Researchers: Martin Benning, Matthias Ehrhardt, Georg Maierhofer, Carola-Bibiane Schönlieb, Ferdia Sherry
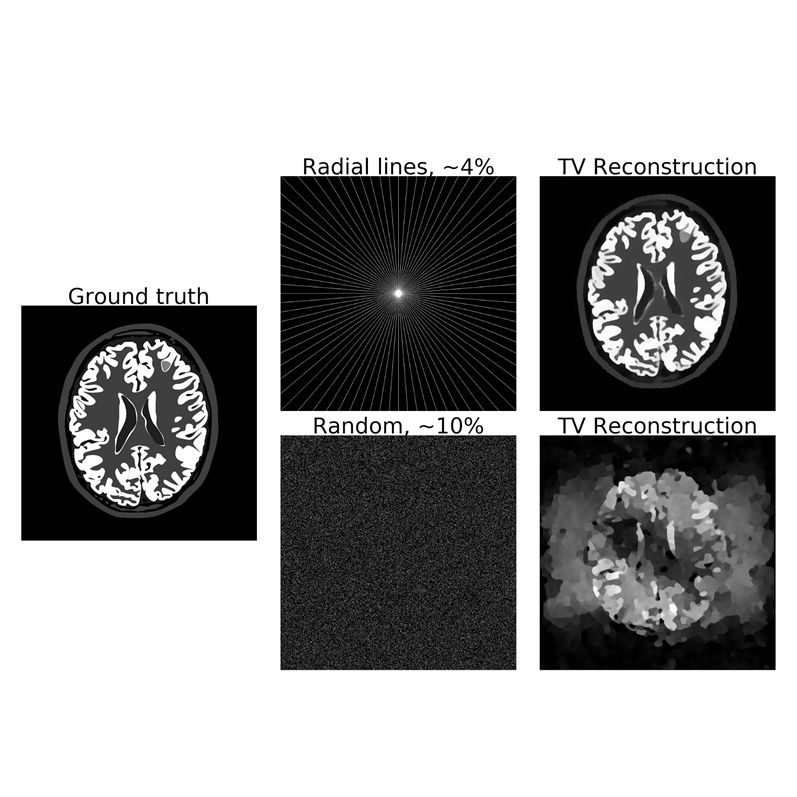
Measurements taken by an MRI machine can be modelled as samples of the Fourier transform of the image that is to be recovered. To accelerate acquisition (in the interest of patient comfort, reduction of motion artifacts etc.), one can choose not to measure all samples but instead measure at a sparsely chosen subsample of the frequencies. When the sampling pattern is suitably chosen (the attached image shows the effect the sampling pattern can have on the reconstruction quality) and an appropriate nonlinear reconstruction algorithm is used (such as reconstruction by solving a total variation regularised least squares problem) this approach gives rise to adequate images in much shorter time than it would take if the Fourier transform was fully sampled. In this project, the goal is to learn a suitable sparse sampling pattern for a given class of images using a training set of fully sampled data that is representative for this class. One way of doing this is by solving a bilevel optimisation problem, in which the upper level problem measures the reconstruction quality and penalises the lack of sparsity in the sampling pattern and the lower level problems are (smoothed versions of) a regularised least squares problem applied to the training set
examples. The bilevel optimisation problem is hard (in the sense that it is nonconvex) but it can be seen as a smooth optimisation problem with box constraints which makes it amenable to the use of the LBFGS-B optimisation algorithm.